Auto Thresholded cartesian reconstruction
Contents
Note
Click here to download the full example code or to run this example in your browser via Binder
Auto Thresholded cartesian reconstruction#
Author: Chaithya G R / Pierre-Antoine Comby
In this tutorial we will reconstruct an MRI image from the sparse kspace measurements.
Import neuroimaging data#
We use the toy datasets available in pysap, more specifically a 2D brain slice and the cartesian acquisition scheme.
Package import
import matplotlib.pyplot as plt
import numpy as np
from modopt.math.metrics import snr, ssim
from modopt.opt.linear import Identity
# Third party import
from modopt.opt.proximity import SparseThreshold
from mri.operators import FFT, WaveletN
from mri.operators.proximity.weighted import AutoWeightedSparseThreshold
from mri.operators.utils import convert_mask_to_locations
from mri.reconstructors import SingleChannelReconstructor
from pysap.data import get_sample_data
image = get_sample_data('2d-mri')
print(image.data.min(), image.data.max())
image = image.data
image /= np.max(image)
mask = get_sample_data("cartesian-mri-mask")
# Get the locations of the kspace samples
kspace_loc = convert_mask_to_locations(mask.data)
# Generate the subsampled kspace
fourier_op = FFT(mask=mask, shape=image.shape)
kspace_data = fourier_op.op(image)
# Zero order solution
image_rec0 = np.abs(fourier_op.adj_op(kspace_data))
# Calculate SSIM
base_ssim = ssim(image_rec0, image)
print(base_ssim)
Out:
9.5823815e-08 2.518473e-05
0.7228762359967604
POGM optimization#
We now want to refine the zero order solution using an accelerated Proximal Gradient Descent algorithm (FISTA or POGM). The cost function is set to Proximity Cost + Gradient Cost
# Setup the operators
linear_op = WaveletN(wavelet_name="sym8", nb_scales=3)
# Manual tweak of the regularisation parameter
regularizer_op = SparseThreshold(Identity(), 2e-3, thresh_type="soft")
# Setup Reconstructor
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
# Start Reconstruction
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_data,
optimization_alg='pogm',
num_iterations=100,
cost_op_kwargs={"cost_interval":None},
metric_call_period=1,
metrics = {
"snr":{
"metric": snr,
"mapping": {"x_new":"test"},
"cst_kwargs": {"ref": image},
"early_stopping":False,
},
"ssim":{
"metric": ssim,
"mapping": {"x_new":"test"},
"cst_kwargs": {"ref": image},
"early_stopping": False,
}
}
)
image_rec = np.abs(x_final)
# image_rec.show()
# Calculate SSIM
recon_ssim = ssim(image_rec, image)
recon_snr= snr(image_rec, image)
print('The Reconstruction SSIM is : ' + str(recon_ssim))
print('The Reconstruction SNR is : ' + str(recon_snr))
Out:
WARNING: Making input data immutable.
Lipschitz constant is 1.1
The lipschitz constraint is satisfied
WARNING: Making input data immutable.
- mu: 0.002
- lipschitz constant: 1.1
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7f3bd11c5870> - 4
- max iterations: 100
- image variable shape: (1, 512, 512)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%|1 | 1/100 [00:00<00:11, 8.66it/s]
2%|2 | 2/100 [00:00<00:11, 8.60it/s]
3%|3 | 3/100 [00:00<00:11, 8.54it/s]
4%|4 | 4/100 [00:00<00:11, 8.54it/s]
5%|5 | 5/100 [00:00<00:11, 8.56it/s]
6%|6 | 6/100 [00:00<00:10, 8.58it/s]
7%|7 | 7/100 [00:00<00:10, 8.57it/s]
8%|8 | 8/100 [00:00<00:10, 8.60it/s]
9%|9 | 9/100 [00:01<00:10, 8.60it/s]
10%|# | 10/100 [00:01<00:10, 8.58it/s]
11%|#1 | 11/100 [00:01<00:10, 8.58it/s]
12%|#2 | 12/100 [00:01<00:10, 8.53it/s]
13%|#3 | 13/100 [00:01<00:10, 8.53it/s]
14%|#4 | 14/100 [00:01<00:10, 8.55it/s]
15%|#5 | 15/100 [00:01<00:09, 8.56it/s]
16%|#6 | 16/100 [00:01<00:09, 8.56it/s]
17%|#7 | 17/100 [00:01<00:09, 8.57it/s]
18%|#8 | 18/100 [00:02<00:09, 8.59it/s]
19%|#9 | 19/100 [00:02<00:09, 8.60it/s]
20%|## | 20/100 [00:02<00:09, 8.59it/s]
21%|##1 | 21/100 [00:02<00:09, 8.60it/s]
22%|##2 | 22/100 [00:02<00:09, 8.59it/s]
23%|##3 | 23/100 [00:02<00:08, 8.61it/s]
24%|##4 | 24/100 [00:02<00:08, 8.60it/s]
25%|##5 | 25/100 [00:02<00:08, 8.58it/s]
26%|##6 | 26/100 [00:03<00:08, 8.58it/s]
27%|##7 | 27/100 [00:03<00:08, 8.57it/s]
28%|##8 | 28/100 [00:03<00:08, 8.61it/s]
29%|##9 | 29/100 [00:03<00:08, 8.60it/s]
30%|### | 30/100 [00:03<00:08, 8.58it/s]
31%|###1 | 31/100 [00:03<00:08, 8.58it/s]
32%|###2 | 32/100 [00:03<00:07, 8.59it/s]
33%|###3 | 33/100 [00:03<00:07, 8.53it/s]
34%|###4 | 34/100 [00:03<00:07, 8.54it/s]
35%|###5 | 35/100 [00:04<00:07, 8.55it/s]
36%|###6 | 36/100 [00:04<00:07, 8.59it/s]
37%|###7 | 37/100 [00:04<00:07, 8.58it/s]
38%|###8 | 38/100 [00:04<00:07, 8.59it/s]
39%|###9 | 39/100 [00:04<00:07, 8.60it/s]
40%|#### | 40/100 [00:04<00:06, 8.60it/s]
41%|####1 | 41/100 [00:04<00:06, 8.65it/s]
42%|####2 | 42/100 [00:04<00:06, 8.60it/s]
43%|####3 | 43/100 [00:05<00:06, 8.59it/s]
44%|####4 | 44/100 [00:05<00:06, 8.57it/s]
45%|####5 | 45/100 [00:05<00:06, 8.59it/s]
46%|####6 | 46/100 [00:05<00:06, 8.61it/s]
47%|####6 | 47/100 [00:05<00:06, 8.60it/s]
48%|####8 | 48/100 [00:05<00:06, 8.59it/s]
49%|####9 | 49/100 [00:05<00:05, 8.53it/s]
50%|##### | 50/100 [00:05<00:05, 8.54it/s]
51%|#####1 | 51/100 [00:05<00:05, 8.60it/s]
52%|#####2 | 52/100 [00:06<00:05, 8.62it/s]
53%|#####3 | 53/100 [00:06<00:05, 8.62it/s]
54%|#####4 | 54/100 [00:06<00:05, 8.61it/s]
55%|#####5 | 55/100 [00:06<00:05, 8.60it/s]
56%|#####6 | 56/100 [00:06<00:05, 8.61it/s]
57%|#####6 | 57/100 [00:06<00:04, 8.61it/s]
58%|#####8 | 58/100 [00:06<00:04, 8.62it/s]
59%|#####8 | 59/100 [00:06<00:04, 8.61it/s]
60%|###### | 60/100 [00:06<00:04, 8.60it/s]
61%|######1 | 61/100 [00:07<00:04, 8.61it/s]
62%|######2 | 62/100 [00:07<00:04, 8.61it/s]
63%|######3 | 63/100 [00:07<00:04, 8.62it/s]
64%|######4 | 64/100 [00:07<00:04, 8.60it/s]
65%|######5 | 65/100 [00:07<00:04, 8.59it/s]
66%|######6 | 66/100 [00:07<00:03, 8.60it/s]
67%|######7 | 67/100 [00:07<00:03, 8.58it/s]
68%|######8 | 68/100 [00:07<00:03, 8.58it/s]
69%|######9 | 69/100 [00:08<00:03, 8.61it/s]
70%|####### | 70/100 [00:08<00:03, 8.61it/s]
71%|#######1 | 71/100 [00:08<00:03, 8.60it/s]
72%|#######2 | 72/100 [00:08<00:03, 8.61it/s]
73%|#######3 | 73/100 [00:08<00:03, 8.62it/s]
74%|#######4 | 74/100 [00:08<00:03, 8.61it/s]
75%|#######5 | 75/100 [00:08<00:02, 8.58it/s]
76%|#######6 | 76/100 [00:08<00:02, 8.58it/s]
77%|#######7 | 77/100 [00:08<00:02, 8.60it/s]
78%|#######8 | 78/100 [00:09<00:02, 8.60it/s]
79%|#######9 | 79/100 [00:09<00:02, 8.59it/s]
80%|######## | 80/100 [00:09<00:02, 8.59it/s]
81%|########1 | 81/100 [00:09<00:02, 8.61it/s]
82%|########2 | 82/100 [00:09<00:02, 8.63it/s]
83%|########2 | 83/100 [00:09<00:01, 8.65it/s]
84%|########4 | 84/100 [00:09<00:01, 8.64it/s]
85%|########5 | 85/100 [00:09<00:01, 8.65it/s]
86%|########6 | 86/100 [00:10<00:01, 8.63it/s]
87%|########7 | 87/100 [00:10<00:01, 8.65it/s]
88%|########8 | 88/100 [00:10<00:01, 8.63it/s]
89%|########9 | 89/100 [00:10<00:01, 8.61it/s]
90%|######### | 90/100 [00:10<00:01, 8.61it/s]
91%|#########1| 91/100 [00:10<00:01, 8.59it/s]
92%|#########2| 92/100 [00:10<00:00, 8.60it/s]
93%|#########3| 93/100 [00:10<00:00, 8.56it/s]
94%|#########3| 94/100 [00:10<00:00, 8.49it/s]
95%|#########5| 95/100 [00:11<00:00, 8.48it/s]
96%|#########6| 96/100 [00:11<00:00, 8.52it/s]
97%|#########7| 97/100 [00:11<00:00, 8.52it/s]
98%|#########8| 98/100 [00:11<00:00, 8.56it/s]
99%|#########9| 99/100 [00:11<00:00, 8.59it/s]
100%|##########| 100/100 [00:11<00:00, 8.58it/s]
100%|##########| 100/100 [00:11<00:00, 8.59it/s]
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 11.643497677054256 seconds
----------------------------------------
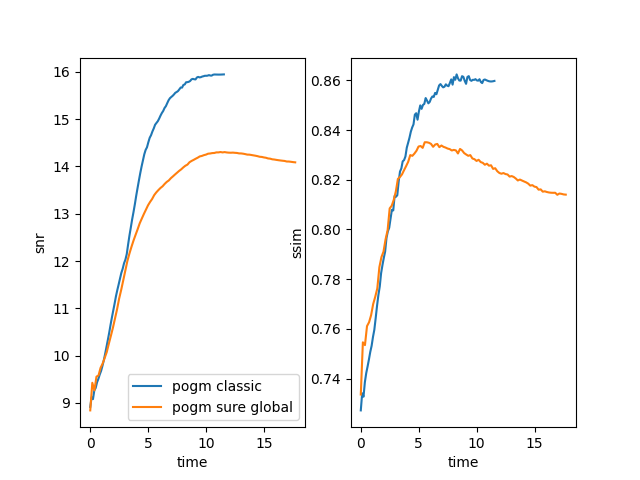
The Reconstruction SSIM is : 0.8597496784357197
The Reconstruction SNR is : 15.947746555163501
Threshold estimation using SURE#
_w = None
def static_weight(w, idx):
print(np.unique(w))
return w
# Setup the operators
linear_op = WaveletN(wavelet_name="sym8", nb_scale=3,padding_mode="periodization")
coeffs = linear_op.op(image_rec0)
print(linear_op.coeffs_shape)
# Here we don't manually setup the regularisation weights, but use statistics on the wavelet details coefficients
regularizer_op = AutoWeightedSparseThreshold(
linear_op.coeffs_shape, linear=Identity(),
update_period=0, # the weight is updated only once.
sigma_range="global",
thresh_range="global",
threshold_estimation="sure",
thresh_type="soft",
)
# Setup Reconstructor
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
# Start Reconstruction
x_final, costs, metrics2 = reconstructor.reconstruct(
kspace_data=kspace_data,
optimization_alg='pogm',
num_iterations=100,
metric_call_period=1,
cost_op_kwargs={"cost_interval":None},
metrics = {
"snr":{
"metric": snr,
"mapping": {"x_new":"test"},
"cst_kwargs": {"ref": image},
"early_stopping":False,
},
"ssim":{
"metric": ssim,
"mapping": {"x_new":"test"},
"cst_kwargs": {"ref": image},
"early_stopping": False,
},
"cost_grad":{
"metric": lambda x: reconstructor.gradient_op.cost(linear_op.op(x)),
"mapping": {"x_new":"x"},
"cst_kwargs": {},
"early_stopping": False,
},
"cost_prox":{
"metric": lambda x: reconstructor.prox_op.cost(linear_op.op(x)),
"mapping": {"x_new":"x"},
"cst_kwargs": {},
"early_stopping": False,
}
}
)
image_rec2 = np.abs(x_final)
# image_rec.show()
# Calculate SSIM
recon_ssim2 = ssim(image_rec2, image)
recon_snr2 = snr(image_rec2, image)
print('The Reconstruction SSIM is : ' + str(recon_ssim2))
print('The Reconstruction SNR is : ' + str(recon_snr2))
plt.subplot(121)
plt.plot(metrics["snr"]["time"], metrics["snr"]["values"], label="pogm classic")
plt.plot(metrics2["snr"]["time"], metrics2["snr"]["values"], label="pogm sure global")
plt.ylabel("snr")
plt.xlabel("time")
plt.legend()
plt.subplot(122)
plt.plot(metrics["ssim"]["time"], metrics["ssim"]["values"])
plt.plot(metrics2["ssim"]["time"], metrics2["ssim"]["values"])
plt.ylabel("ssim")
plt.xlabel("time")
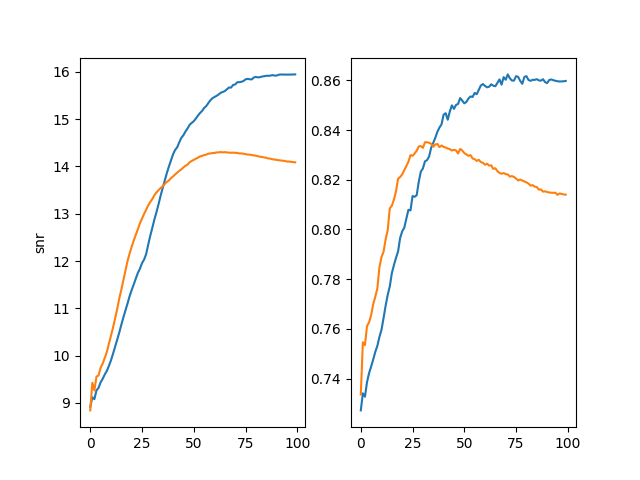
plt.figure()
plt.subplot(121)
plt.plot(metrics["snr"]["index"], metrics["snr"]["values"])
plt.plot(metrics2["snr"]["index"], metrics2["snr"]["values"])
plt.ylabel("snr")
plt.subplot(122)
plt.plot(metrics["ssim"]["index"], metrics["ssim"]["values"])
plt.plot(metrics2["ssim"]["index"], metrics2["ssim"]["values"])
plt.show()
Out:
[(64, 64), (64, 64), (64, 64), (64, 64), (128, 128), (128, 128), (128, 128), (256, 256), (256, 256), (256, 256)]
WARNING: Making input data immutable.
Lipschitz constant is 1.1000001311302186
The lipschitz constraint is satisfied
- mu: [0. 0. 0. ... 0. 0. 0.]
- lipschitz constant: 1.1000001311302186
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7f3a4e93b910> - 3
- max iterations: 100
- image variable shape: (1, 512, 512)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%|1 | 1/100 [00:00<00:17, 5.51it/s]
2%|2 | 2/100 [00:00<00:17, 5.53it/s]
3%|3 | 3/100 [00:00<00:17, 5.58it/s]
4%|4 | 4/100 [00:00<00:17, 5.60it/s]
5%|5 | 5/100 [00:00<00:16, 5.60it/s]
6%|6 | 6/100 [00:01<00:16, 5.63it/s]
7%|7 | 7/100 [00:01<00:16, 5.64it/s]
8%|8 | 8/100 [00:01<00:16, 5.62it/s]
9%|9 | 9/100 [00:01<00:16, 5.62it/s]
10%|# | 10/100 [00:01<00:16, 5.61it/s]
11%|#1 | 11/100 [00:01<00:15, 5.62it/s]
12%|#2 | 12/100 [00:02<00:15, 5.62it/s]
13%|#3 | 13/100 [00:02<00:15, 5.60it/s]
14%|#4 | 14/100 [00:02<00:15, 5.63it/s]
15%|#5 | 15/100 [00:02<00:15, 5.62it/s]
16%|#6 | 16/100 [00:02<00:14, 5.61it/s]
17%|#7 | 17/100 [00:03<00:14, 5.62it/s]
18%|#8 | 18/100 [00:03<00:14, 5.65it/s]
19%|#9 | 19/100 [00:03<00:14, 5.63it/s]
20%|## | 20/100 [00:03<00:14, 5.63it/s]
21%|##1 | 21/100 [00:03<00:13, 5.66it/s]
22%|##2 | 22/100 [00:03<00:13, 5.62it/s]
23%|##3 | 23/100 [00:04<00:13, 5.63it/s]
24%|##4 | 24/100 [00:04<00:13, 5.63it/s]
25%|##5 | 25/100 [00:04<00:13, 5.61it/s]
26%|##6 | 26/100 [00:04<00:13, 5.60it/s]
27%|##7 | 27/100 [00:04<00:13, 5.60it/s]
28%|##8 | 28/100 [00:04<00:12, 5.61it/s]
29%|##9 | 29/100 [00:05<00:12, 5.61it/s]
30%|### | 30/100 [00:05<00:12, 5.62it/s]
31%|###1 | 31/100 [00:05<00:12, 5.61it/s]
32%|###2 | 32/100 [00:05<00:12, 5.62it/s]
33%|###3 | 33/100 [00:05<00:12, 5.58it/s]
34%|###4 | 34/100 [00:06<00:11, 5.56it/s]
35%|###5 | 35/100 [00:06<00:11, 5.56it/s]
36%|###6 | 36/100 [00:06<00:11, 5.55it/s]
37%|###7 | 37/100 [00:06<00:11, 5.55it/s]
38%|###8 | 38/100 [00:06<00:11, 5.56it/s]
39%|###9 | 39/100 [00:06<00:10, 5.58it/s]
40%|#### | 40/100 [00:07<00:10, 5.57it/s]
41%|####1 | 41/100 [00:07<00:10, 5.57it/s]
42%|####2 | 42/100 [00:07<00:10, 5.58it/s]
43%|####3 | 43/100 [00:07<00:10, 5.60it/s]
44%|####4 | 44/100 [00:07<00:10, 5.60it/s]
45%|####5 | 45/100 [00:08<00:09, 5.60it/s]
46%|####6 | 46/100 [00:08<00:09, 5.61it/s]
47%|####6 | 47/100 [00:08<00:09, 5.61it/s]
48%|####8 | 48/100 [00:08<00:09, 5.61it/s]
49%|####9 | 49/100 [00:08<00:09, 5.63it/s]
50%|##### | 50/100 [00:08<00:08, 5.62it/s]
51%|#####1 | 51/100 [00:09<00:08, 5.62it/s]
52%|#####2 | 52/100 [00:09<00:08, 5.63it/s]
53%|#####3 | 53/100 [00:09<00:08, 5.63it/s]
54%|#####4 | 54/100 [00:09<00:08, 5.63it/s]
55%|#####5 | 55/100 [00:09<00:08, 5.60it/s]
56%|#####6 | 56/100 [00:09<00:07, 5.60it/s]
57%|#####6 | 57/100 [00:10<00:07, 5.60it/s]
58%|#####8 | 58/100 [00:10<00:07, 5.58it/s]
59%|#####8 | 59/100 [00:10<00:07, 5.58it/s]
60%|###### | 60/100 [00:10<00:07, 5.59it/s]
61%|######1 | 61/100 [00:10<00:06, 5.59it/s]
62%|######2 | 62/100 [00:11<00:06, 5.59it/s]
63%|######3 | 63/100 [00:11<00:06, 5.62it/s]
64%|######4 | 64/100 [00:11<00:06, 5.60it/s]
65%|######5 | 65/100 [00:11<00:06, 5.61it/s]
66%|######6 | 66/100 [00:11<00:06, 5.60it/s]
67%|######7 | 67/100 [00:11<00:05, 5.60it/s]
68%|######8 | 68/100 [00:12<00:05, 5.60it/s]
69%|######9 | 69/100 [00:12<00:05, 5.60it/s]
70%|####### | 70/100 [00:12<00:05, 5.63it/s]
71%|#######1 | 71/100 [00:12<00:05, 5.62it/s]
72%|#######2 | 72/100 [00:12<00:04, 5.63it/s]
73%|#######3 | 73/100 [00:13<00:04, 5.64it/s]
74%|#######4 | 74/100 [00:13<00:04, 5.64it/s]
75%|#######5 | 75/100 [00:13<00:04, 5.64it/s]
76%|#######6 | 76/100 [00:13<00:04, 5.64it/s]
77%|#######7 | 77/100 [00:13<00:04, 5.62it/s]
78%|#######8 | 78/100 [00:13<00:03, 5.62it/s]
79%|#######9 | 79/100 [00:14<00:03, 5.62it/s]
80%|######## | 80/100 [00:14<00:03, 5.62it/s]
81%|########1 | 81/100 [00:14<00:03, 5.59it/s]
82%|########2 | 82/100 [00:14<00:03, 5.60it/s]
83%|########2 | 83/100 [00:14<00:03, 5.59it/s]
84%|########4 | 84/100 [00:14<00:02, 5.57it/s]
85%|########5 | 85/100 [00:15<00:02, 5.59it/s]
86%|########6 | 86/100 [00:15<00:02, 5.59it/s]
87%|########7 | 87/100 [00:15<00:02, 5.57it/s]
88%|########8 | 88/100 [00:15<00:02, 5.55it/s]
89%|########9 | 89/100 [00:15<00:01, 5.58it/s]
90%|######### | 90/100 [00:16<00:01, 5.59it/s]
91%|#########1| 91/100 [00:16<00:01, 5.60it/s]
92%|#########2| 92/100 [00:16<00:01, 5.60it/s]
93%|#########3| 93/100 [00:16<00:01, 5.59it/s]
94%|#########3| 94/100 [00:16<00:01, 5.60it/s]
95%|#########5| 95/100 [00:16<00:00, 5.56it/s]
96%|#########6| 96/100 [00:17<00:00, 5.56it/s]
97%|#########7| 97/100 [00:17<00:00, 5.52it/s]
98%|#########8| 98/100 [00:17<00:00, 5.50it/s]
99%|#########9| 99/100 [00:17<00:00, 5.51it/s]
100%|##########| 100/100 [00:17<00:00, 5.50it/s]
100%|##########| 100/100 [00:17<00:00, 5.60it/s]
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 17.867400695104152 seconds
----------------------------------------
The Reconstruction SSIM is : 0.8140168579836002
The Reconstruction SNR is : 14.087662909035688
/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/cartesian_reconstruction_auto_threshold.py:198: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
Qualitative results#
def my_imshow(ax, img, title):
ax.imshow(img, cmap="gray")
ax.set_title(title)
ax.axis("off")
fig, axs = plt.subplots(2,2)
my_imshow(axs[0,0], image, "Ground Truth")
my_imshow(axs[0,1], abs(image_rec0), f"Zero Order \n SSIM={base_ssim:.4f}")
my_imshow(axs[1,0], abs(image_rec), f"Fista Classic \n SSIM={recon_ssim:.4f}")
my_imshow(axs[1,1], abs(image_rec2), f"Fista Sure \n SSIM={recon_ssim2:.4f}")
fig.tight_layout()
plt.show()
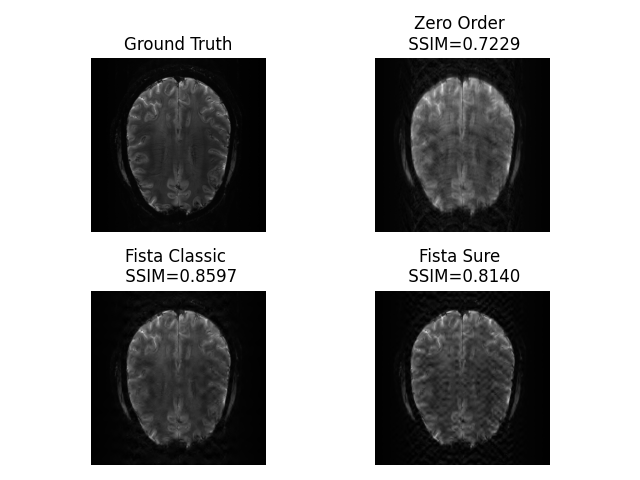
Out:
/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/cartesian_reconstruction_auto_threshold.py:219: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
Total running time of the script: ( 0 minutes 33.467 seconds)