Cartesian Calibrationless Reconstruction using OWL Regularizer
Contents
Note
Click here to download the full example code or to run this example in your browser via Binder
Cartesian Calibrationless Reconstruction using OWL Regularizer#
Author: Chaithya G R
In this tutorial we will reconstruct an MRI image from cartesian kspace measurements.
Import neuroimaging data#
We use the toy datasets available in pysap, more specifically a 2D parallel MRI brain slice on 32 channels and the acquisition cartesian scheme.
Package import
from mri.operators import FFT, WaveletN, OWL
from mri.reconstructors import CalibrationlessReconstructor
from pysap.data import get_sample_data
# Third party import
from modopt.math.metrics import ssim
import numpy as np
import matplotlib.pyplot as plt
Loading input data
cartesian_ref_image = get_sample_data('2d-pmri').data
image = np.linalg.norm(cartesian_ref_image, axis=0)
# Obtain MRI cartesian mask
mask = get_sample_data("cartesian-mri-mask").data
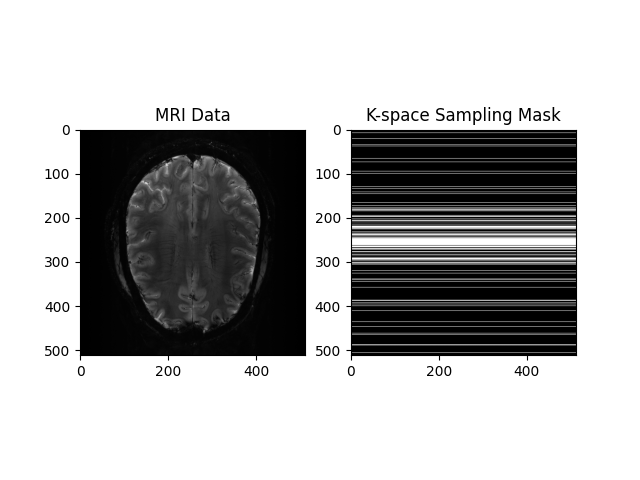
View Input
plt.subplot(1, 2, 1)
plt.imshow(np.abs(image), cmap='gray')
plt.title("MRI Data")
plt.subplot(1, 2, 2)
plt.imshow(mask, cmap='gray')
plt.title("K-space Sampling Mask")
plt.show()
Out:
/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/CalibrationlessReconstruction_OWL_Cartesian.py:42: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
Generate the kspace#
From the 2D brain slice and the acquisition mask, we retrospectively undersample the k-space using a cartesian acquisition mask We then reconstruct the zero order solution as a baseline
# Get the locations of the kspace samples and the associated observations
fourier_op = FFT(mask=mask, shape=image.shape,
n_coils=cartesian_ref_image.shape[0])
kspace_obs = fourier_op.op(cartesian_ref_image)
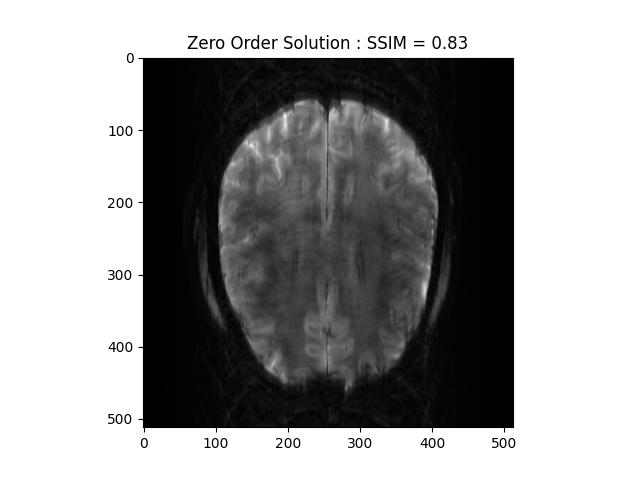
Zero order solution
zero_soln = np.linalg.norm(fourier_op.adj_op(kspace_obs), axis=0)
base_ssim = ssim(zero_soln, image)
plt.imshow(np.abs(zero_soln), cmap='gray')
plt.title('Zero Order Solution : SSIM = ' + str(np.around(base_ssim, 2)))
plt.show()
Out:
/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/CalibrationlessReconstruction_OWL_Cartesian.py:63: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
FISTA optimization#
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost
# Setup the operators
linear_op = WaveletN(
wavelet_name='sym8',
nb_scale=4,
n_coils=cartesian_ref_image.shape[0],
)
coeffs = linear_op.op(cartesian_ref_image)
regularizer_op = OWL(
alpha=1.05e-8,
beta=0,
mode='band_based',
n_coils=cartesian_ref_image.shape[0],
bands_shape=linear_op.coeffs_shape,
)
# Setup Reconstructor
reconstructor = CalibrationlessReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
Out:
WARNING: Making input data immutable.
Lipschitz constant is 1.0999999344348907
The lipschitz constraint is satisfied
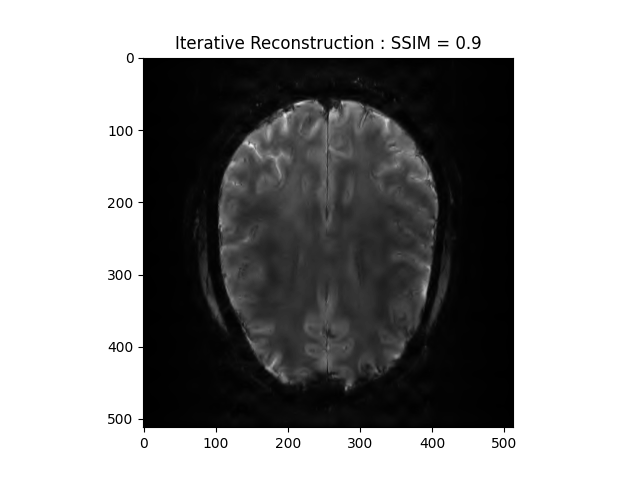
Run the FISTA reconstruction and view results
image_rec, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='fista',
num_iterations=100,
)
image_rec = np.linalg.norm(image_rec, axis=0)
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('Iterative Reconstruction : SSIM = ' + str(np.around(recon_ssim, 2)))
plt.show()
Out:
WARNING: Making input data immutable.
- mu: [<modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec3bbb0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec39990>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec38430>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec3a050>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec39d80>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec38d30>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec396c0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a67d08bb0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4edd0730>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec3b460>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec3b400>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec3ba00>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7f3a4ec39420>]
- lipschitz constant: 1.0999999344348907
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7f3a4ec39f30> - 4
- max iterations: 100
- image variable shape: (512, 512)
- alpha variable shape: (32, 291721)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%|1 | 1/100 [00:03<05:25, 3.29s/it]
2%|2 | 2/100 [00:06<05:21, 3.28s/it]
3%|3 | 3/100 [00:09<05:18, 3.28s/it]
4%|4 | 4/100 [00:13<05:13, 3.27s/it]
5%|5 | 5/100 [00:16<05:10, 3.27s/it]
6%|6 | 6/100 [00:19<05:07, 3.27s/it]
7%|7 | 7/100 [00:22<05:03, 3.27s/it]
8%|8 | 8/100 [00:26<05:00, 3.26s/it]
9%|9 | 9/100 [00:29<04:56, 3.26s/it]
10%|# | 10/100 [00:32<04:53, 3.26s/it]
11%|#1 | 11/100 [00:35<04:49, 3.25s/it]
12%|#2 | 12/100 [00:39<04:46, 3.25s/it]
13%|#3 | 13/100 [00:42<04:43, 3.26s/it]
14%|#4 | 14/100 [00:45<04:40, 3.26s/it]
15%|#5 | 15/100 [00:48<04:37, 3.26s/it]
16%|#6 | 16/100 [00:52<04:33, 3.26s/it]
17%|#7 | 17/100 [00:55<04:30, 3.26s/it]
18%|#8 | 18/100 [00:58<04:26, 3.25s/it]
19%|#9 | 19/100 [01:02<04:24, 3.27s/it]
20%|## | 20/100 [01:05<04:21, 3.27s/it]
21%|##1 | 21/100 [01:08<04:18, 3.28s/it]
22%|##2 | 22/100 [01:11<04:15, 3.28s/it]
23%|##3 | 23/100 [01:15<04:11, 3.27s/it]
24%|##4 | 24/100 [01:18<04:08, 3.26s/it]
25%|##5 | 25/100 [01:21<04:04, 3.26s/it]
26%|##6 | 26/100 [01:24<04:01, 3.27s/it]
27%|##7 | 27/100 [01:28<03:59, 3.27s/it]
28%|##8 | 28/100 [01:31<03:55, 3.27s/it]
29%|##9 | 29/100 [01:34<03:52, 3.28s/it]
30%|### | 30/100 [01:37<03:48, 3.27s/it]
31%|###1 | 31/100 [01:41<03:45, 3.27s/it]
32%|###2 | 32/100 [01:44<03:42, 3.27s/it]
33%|###3 | 33/100 [01:47<03:39, 3.27s/it]
34%|###4 | 34/100 [01:51<03:35, 3.27s/it]
35%|###5 | 35/100 [01:54<03:32, 3.27s/it]
36%|###6 | 36/100 [01:57<03:29, 3.27s/it]
37%|###7 | 37/100 [02:00<03:25, 3.27s/it]
38%|###8 | 38/100 [02:04<03:21, 3.26s/it]
39%|###9 | 39/100 [02:07<03:19, 3.27s/it]
40%|#### | 40/100 [02:10<03:16, 3.27s/it]
41%|####1 | 41/100 [02:13<03:12, 3.27s/it]
42%|####2 | 42/100 [02:17<03:09, 3.27s/it]
43%|####3 | 43/100 [02:20<03:06, 3.28s/it]
44%|####4 | 44/100 [02:23<03:03, 3.27s/it]
45%|####5 | 45/100 [02:27<03:00, 3.28s/it]
46%|####6 | 46/100 [02:30<02:56, 3.27s/it]
47%|####6 | 47/100 [02:33<02:53, 3.27s/it]
48%|####8 | 48/100 [02:36<02:50, 3.27s/it]
49%|####9 | 49/100 [02:40<02:46, 3.27s/it]
50%|##### | 50/100 [02:43<02:43, 3.28s/it]
51%|#####1 | 51/100 [02:46<02:40, 3.28s/it]
52%|#####2 | 52/100 [02:49<02:37, 3.28s/it]
53%|#####3 | 53/100 [02:53<02:33, 3.27s/it]
54%|#####4 | 54/100 [02:56<02:30, 3.27s/it]
55%|#####5 | 55/100 [02:59<02:27, 3.27s/it]
56%|#####6 | 56/100 [03:03<02:24, 3.28s/it]
57%|#####6 | 57/100 [03:06<02:21, 3.28s/it]
58%|#####8 | 58/100 [03:09<02:17, 3.28s/it]
59%|#####8 | 59/100 [03:12<02:14, 3.28s/it]
60%|###### | 60/100 [03:16<02:10, 3.27s/it]
61%|######1 | 61/100 [03:19<02:07, 3.28s/it]
62%|######2 | 62/100 [03:22<02:04, 3.27s/it]
63%|######3 | 63/100 [03:26<02:01, 3.27s/it]
64%|######4 | 64/100 [03:29<01:57, 3.27s/it]
65%|######5 | 65/100 [03:32<01:54, 3.27s/it]
66%|######6 | 66/100 [03:35<01:51, 3.27s/it]
67%|######7 | 67/100 [03:39<01:47, 3.27s/it]
68%|######8 | 68/100 [03:42<01:44, 3.27s/it]
69%|######9 | 69/100 [03:45<01:41, 3.27s/it]
70%|####### | 70/100 [03:48<01:38, 3.27s/it]
71%|#######1 | 71/100 [03:52<01:34, 3.27s/it]
72%|#######2 | 72/100 [03:55<01:31, 3.27s/it]
73%|#######3 | 73/100 [03:58<01:28, 3.28s/it]
74%|#######4 | 74/100 [04:02<01:25, 3.29s/it]
75%|#######5 | 75/100 [04:05<01:22, 3.29s/it]
76%|#######6 | 76/100 [04:08<01:18, 3.29s/it]
77%|#######7 | 77/100 [04:11<01:15, 3.29s/it]
78%|#######8 | 78/100 [04:15<01:12, 3.29s/it]
79%|#######9 | 79/100 [04:18<01:09, 3.29s/it]
80%|######## | 80/100 [04:21<01:05, 3.28s/it]
81%|########1 | 81/100 [04:25<01:02, 3.29s/it]
82%|########2 | 82/100 [04:28<00:59, 3.29s/it]
83%|########2 | 83/100 [04:31<00:55, 3.29s/it]
84%|########4 | 84/100 [04:34<00:52, 3.29s/it]
85%|########5 | 85/100 [04:38<00:49, 3.29s/it]
86%|########6 | 86/100 [04:41<00:46, 3.29s/it]
87%|########7 | 87/100 [04:44<00:42, 3.29s/it]
88%|########8 | 88/100 [04:48<00:39, 3.28s/it]
89%|########9 | 89/100 [04:51<00:36, 3.28s/it]
90%|######### | 90/100 [04:54<00:32, 3.27s/it]
91%|#########1| 91/100 [04:57<00:29, 3.29s/it]
92%|#########2| 92/100 [05:01<00:26, 3.29s/it]
93%|#########3| 93/100 [05:04<00:23, 3.29s/it]
94%|#########3| 94/100 [05:07<00:19, 3.29s/it]
95%|#########5| 95/100 [05:11<00:16, 3.29s/it]
96%|#########6| 96/100 [05:14<00:13, 3.28s/it]
97%|#########7| 97/100 [05:17<00:09, 3.29s/it]
98%|#########8| 98/100 [05:20<00:06, 3.28s/it]
99%|#########9| 99/100 [05:24<00:03, 3.29s/it]
100%|##########| 100/100 [05:27<00:00, 3.29s/it]
100%|##########| 100/100 [05:27<00:00, 3.27s/it]
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 327.494948472362 seconds
----------------------------------------
/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/CalibrationlessReconstruction_OWL_Cartesian.py:105: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
Total running time of the script: ( 6 minutes 20.463 seconds)
