Neuroimaging cartesian reconstruction

Author: Chaithya G R

In this tutorial we will reconstruct an MRI image from the sparse kspace measurements.

Import neuroimaging data

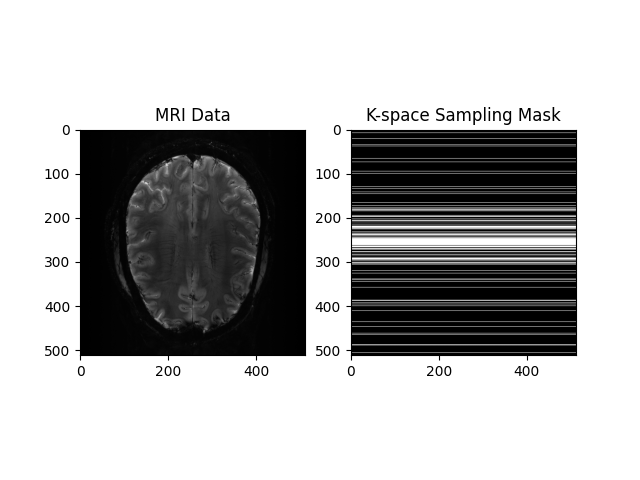
We use the toy datasets available in pysap, more specifically a 2D brain slice and the cartesian acquisition scheme.

Package import

from mri.operators import FFT, WaveletN
from mri.operators.utils import convert_mask_to_locations
from mri.reconstructors import SingleChannelReconstructor
from pysap.data import get_sample_data

# Third party import
from modopt.opt.proximity import SparseThreshold
from modopt.opt.linear import Identity
from modopt.math.metrics import ssim
import numpy as np
import matplotlib.pyplot as plt

Loading input data

image = get_sample_data('2d-mri')
# Obtain K-Space Cartesian Mask
mask = get_sample_data("cartesian-mri-mask")

View Input

plt.subplot(1, 2, 1)
plt.imshow(np.abs(image), cmap='gray')
plt.title("MRI Data")
plt.subplot(1, 2, 2)
plt.imshow(mask, cmap='gray')
plt.title("K-space Sampling Mask")
plt.show()

Out:

/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/cartesian_reconstruction.py:45: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  plt.show()

Generate the kspace

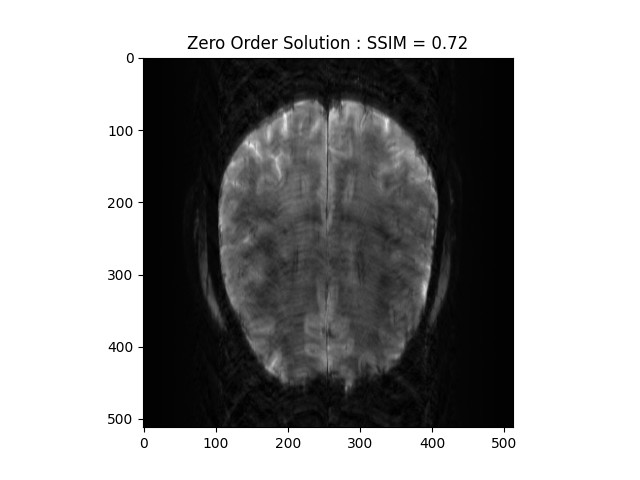
From the 2D brain slice and the acquisition mask, we retrospectively undersample the k-space using a cartesian acquisition mask We then reconstruct the zero order solution as a baseline

# Get the locations of the kspace samples
kspace_loc = convert_mask_to_locations(mask.data)
# Generate the subsampled kspace
fourier_op = FFT(samples=kspace_loc, shape=image.shape)
kspace_data = fourier_op.op(image)

Zero order solution

zero_soln = fourier_op.adj_op(kspace_data)
base_ssim = ssim(zero_soln, image)
plt.imshow(np.abs(zero_soln), cmap='gray')
plt.title('Zero Order Solution : SSIM = ' + str(np.around(base_ssim, 2)))
plt.show()

Out:

/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/cartesian_reconstruction.py:68: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  plt.show()

FISTA optimization

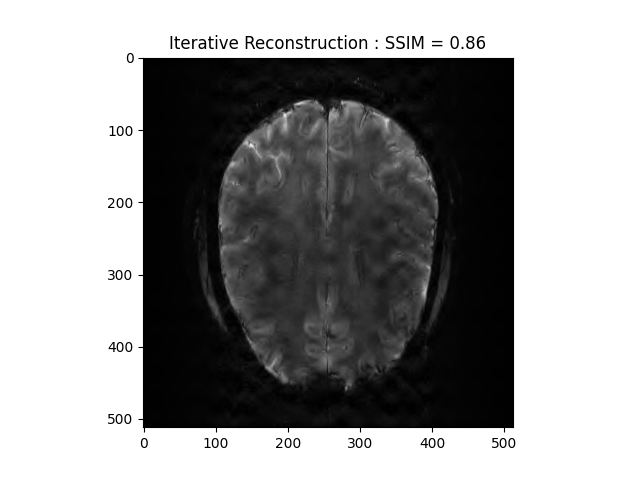
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost

# Setup the operators
linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
regularizer_op = SparseThreshold(Identity(), 2 * 1e-7, thresh_type="soft")
# Setup Reconstructor
reconstructor = SingleChannelReconstructor(
    fourier_op=fourier_op,
    linear_op=linear_op,
    regularizer_op=regularizer_op,
    gradient_formulation='synthesis',
    verbose=1,
)

Out:

WARNING: Making input data immutable.
Lipschitz constant is 1.0999999146827621
The lipschitz constraint is satisfied

Start Reconstruction

image_rec, costs, metrics = reconstructor.reconstruct(
    kspace_data=kspace_data,
    optimization_alg='fista',
    num_iterations=200,
)
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('Iterative Reconstruction : SSIM = ' + str(np.around(recon_ssim, 2)))
plt.show()

Out:

WARNING: Making input data immutable.
 - mu:  2e-07
 - lipschitz constant:  1.0999999146827621
 - data:  (512, 512)
 - wavelet:  <mri.operators.linear.wavelet.WaveletN object at 0x7f3a681cb2e0> - 4
 - max iterations:  200
 - image variable shape:  (512, 512)
 - alpha variable shape:  (291721,)
----------------------------------------
Starting optimization...

  0%|          | 0/200 [00:00<?, ?it/s]
  0%|          | 1/200 [00:00<00:24,  8.06it/s]
  2%|1         | 3/200 [00:00<00:19, 10.20it/s]
  2%|2         | 5/200 [00:00<00:18, 10.80it/s]
  4%|3         | 7/200 [00:00<00:17, 11.03it/s]
  4%|4         | 9/200 [00:00<00:17, 11.15it/s]
  6%|5         | 11/200 [00:01<00:16, 11.18it/s]
  6%|6         | 13/200 [00:01<00:16, 11.28it/s]
  8%|7         | 15/200 [00:01<00:16, 11.34it/s]
  8%|8         | 17/200 [00:01<00:16, 11.31it/s]
 10%|9         | 19/200 [00:01<00:15, 11.41it/s]
 10%|#         | 21/200 [00:01<00:15, 11.43it/s]
 12%|#1        | 23/200 [00:02<00:15, 11.44it/s]
 12%|#2        | 25/200 [00:02<00:15, 11.41it/s]
 14%|#3        | 27/200 [00:02<00:15, 11.38it/s]
 14%|#4        | 29/200 [00:02<00:15, 11.35it/s]
 16%|#5        | 31/200 [00:02<00:14, 11.38it/s]
 16%|#6        | 33/200 [00:02<00:14, 11.30it/s]
 18%|#7        | 35/200 [00:03<00:14, 11.31it/s]
 18%|#8        | 37/200 [00:03<00:14, 11.37it/s]
 20%|#9        | 39/200 [00:03<00:14, 11.40it/s]
 20%|##        | 41/200 [00:03<00:13, 11.39it/s]
 22%|##1       | 43/200 [00:03<00:13, 11.32it/s]
 22%|##2       | 45/200 [00:03<00:13, 11.38it/s]
 24%|##3       | 47/200 [00:04<00:13, 11.37it/s]
 24%|##4       | 49/200 [00:04<00:13, 11.44it/s]
 26%|##5       | 51/200 [00:04<00:13, 11.36it/s]
 26%|##6       | 53/200 [00:04<00:12, 11.39it/s]
 28%|##7       | 55/200 [00:04<00:12, 11.44it/s]
 28%|##8       | 57/200 [00:05<00:12, 11.45it/s]
 30%|##9       | 59/200 [00:05<00:12, 11.49it/s]
 30%|###       | 61/200 [00:05<00:12, 11.49it/s]
 32%|###1      | 63/200 [00:05<00:11, 11.45it/s]
 32%|###2      | 65/200 [00:05<00:11, 11.43it/s]
 34%|###3      | 67/200 [00:05<00:11, 11.42it/s]
 34%|###4      | 69/200 [00:06<00:11, 11.43it/s]
 36%|###5      | 71/200 [00:06<00:11, 11.40it/s]
 36%|###6      | 73/200 [00:06<00:11, 11.39it/s]
 38%|###7      | 75/200 [00:06<00:10, 11.38it/s]
 38%|###8      | 77/200 [00:06<00:10, 11.39it/s]
 40%|###9      | 79/200 [00:06<00:10, 11.35it/s]
 40%|####      | 81/200 [00:07<00:10, 11.37it/s]
 42%|####1     | 83/200 [00:07<00:10, 11.45it/s]
 42%|####2     | 85/200 [00:07<00:10, 11.40it/s]
 44%|####3     | 87/200 [00:07<00:09, 11.38it/s]
 44%|####4     | 89/200 [00:07<00:09, 11.42it/s]
 46%|####5     | 91/200 [00:08<00:09, 11.46it/s]
 46%|####6     | 93/200 [00:08<00:09, 11.39it/s]
 48%|####7     | 95/200 [00:08<00:09, 11.38it/s]
 48%|####8     | 97/200 [00:08<00:09, 11.35it/s]
 50%|####9     | 99/200 [00:08<00:08, 11.31it/s]
 50%|#####     | 101/200 [00:08<00:08, 11.33it/s]
 52%|#####1    | 103/200 [00:09<00:08, 11.37it/s]
 52%|#####2    | 105/200 [00:09<00:08, 11.35it/s]
 54%|#####3    | 107/200 [00:09<00:08, 11.37it/s]
 55%|#####4    | 109/200 [00:09<00:07, 11.39it/s]
 56%|#####5    | 111/200 [00:09<00:07, 11.49it/s]
 56%|#####6    | 113/200 [00:09<00:07, 11.48it/s]
 57%|#####7    | 115/200 [00:10<00:07, 11.47it/s]
 58%|#####8    | 117/200 [00:10<00:07, 11.41it/s]
 60%|#####9    | 119/200 [00:10<00:07, 11.47it/s]
 60%|######    | 121/200 [00:10<00:06, 11.47it/s]
 62%|######1   | 123/200 [00:10<00:06, 11.45it/s]
 62%|######2   | 125/200 [00:11<00:06, 11.37it/s]
 64%|######3   | 127/200 [00:11<00:06, 11.38it/s]
 64%|######4   | 129/200 [00:11<00:06, 11.36it/s]
 66%|######5   | 131/200 [00:11<00:06, 11.40it/s]
 66%|######6   | 133/200 [00:11<00:05, 11.45it/s]
 68%|######7   | 135/200 [00:11<00:05, 11.44it/s]
 68%|######8   | 137/200 [00:12<00:05, 11.42it/s]
 70%|######9   | 139/200 [00:12<00:05, 11.42it/s]
 70%|#######   | 141/200 [00:12<00:05, 11.37it/s]
 72%|#######1  | 143/200 [00:12<00:04, 11.41it/s]
 72%|#######2  | 145/200 [00:12<00:04, 11.42it/s]
 74%|#######3  | 147/200 [00:12<00:04, 11.39it/s]
 74%|#######4  | 149/200 [00:13<00:04, 11.43it/s]
 76%|#######5  | 151/200 [00:13<00:04, 11.37it/s]
 76%|#######6  | 153/200 [00:13<00:04, 11.39it/s]
 78%|#######7  | 155/200 [00:13<00:03, 11.48it/s]
 78%|#######8  | 157/200 [00:13<00:03, 11.46it/s]
 80%|#######9  | 159/200 [00:13<00:03, 11.44it/s]
 80%|########  | 161/200 [00:14<00:03, 11.40it/s]
 82%|########1 | 163/200 [00:14<00:03, 11.39it/s]
 82%|########2 | 165/200 [00:14<00:03, 11.43it/s]
 84%|########3 | 167/200 [00:14<00:02, 11.39it/s]
 84%|########4 | 169/200 [00:14<00:02, 11.42it/s]
 86%|########5 | 171/200 [00:15<00:02, 11.38it/s]
 86%|########6 | 173/200 [00:15<00:02, 11.39it/s]
 88%|########7 | 175/200 [00:15<00:02, 11.41it/s]
 88%|########8 | 177/200 [00:15<00:02, 11.39it/s]
 90%|########9 | 179/200 [00:15<00:01, 11.37it/s]
 90%|######### | 181/200 [00:15<00:01, 11.34it/s]
 92%|#########1| 183/200 [00:16<00:01, 11.34it/s]
 92%|#########2| 185/200 [00:16<00:01, 11.30it/s]
 94%|#########3| 187/200 [00:16<00:01, 11.33it/s]
 94%|#########4| 189/200 [00:16<00:00, 11.43it/s]
 96%|#########5| 191/200 [00:16<00:00, 11.46it/s]
 96%|#########6| 193/200 [00:16<00:00, 11.40it/s]
 98%|#########7| 195/200 [00:17<00:00, 11.41it/s]
 98%|#########8| 197/200 [00:17<00:00, 11.41it/s]
100%|#########9| 199/200 [00:17<00:00, 11.35it/s]
100%|##########| 200/200 [00:17<00:00, 11.38it/s]
 - final iteration number:  200
 - final log10 cost value:  6.0
 - converged:  False
Done.
Execution time:  17.58240639604628  seconds
----------------------------------------
/volatile/Chaithya/actions-runner/_work/pysap/pysap/examples/pysap-mri/cartesian_reconstruction.py:98: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  plt.show()